Sudoku rules and strategies
Sudoku is a mathematical logic game consisting of a grid of 9×9 squares. Players need to deduce the values of the other squares based on the given numbers in the grid. The game is designed so that there is only one solution with at least 17 pre-filled numbers provided by the game designer.
This game requires only logical thinking ability, and is unrelated to arithmetic, making it suitable for people who are not good at math. Although the gameplay is simple, the numbers provided can vary greatly, making Sudoku a good method for exercising the brain, according to many educators.
Sudoku was invented by American puzzle inventor Howard Garns in 1979, and was further developed by Japanese publisher Nikoli in 1986, with the name meaning “independent numbers”.
Over the years, Sudoku has spread worldwide.
Sudoku Game Rules:
The goal of Sudoku is to fill a 9×9 grid with numbers so that each row, column, and 3×3 sub-grid contains the numbers 1 to 9. At the beginning of the game, some squares are already filled with numbers. Players must use logic to fill in the missing numbers and solve the puzzle. Each Sudoku puzzle has only one solution!
The following conditions must be ensured:
- Each row must contain every number from 1-9, without repetition.
- Each column must contain every number from 1-9, without repetition.
- Each sub-grid (outlined by bold black lines, usually 3×3) must contain every number from 1-9, without repetition.
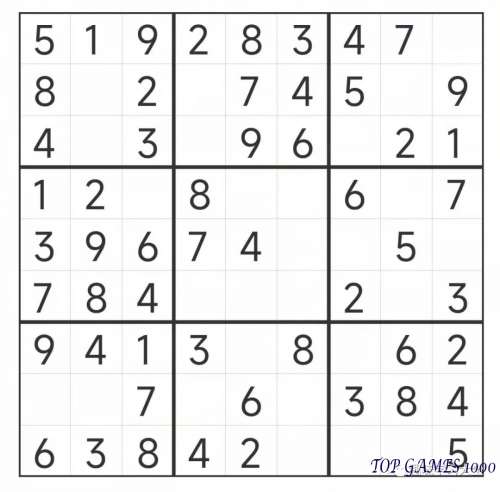
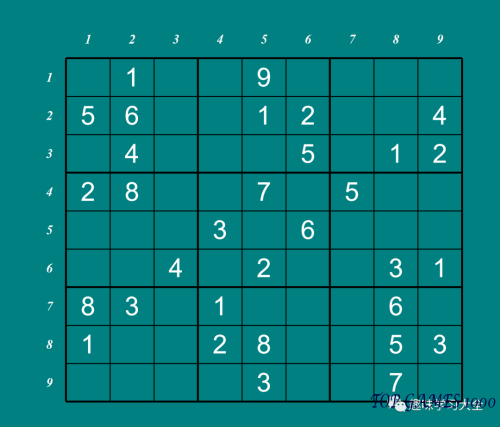
Sudoku Starting Puzzle
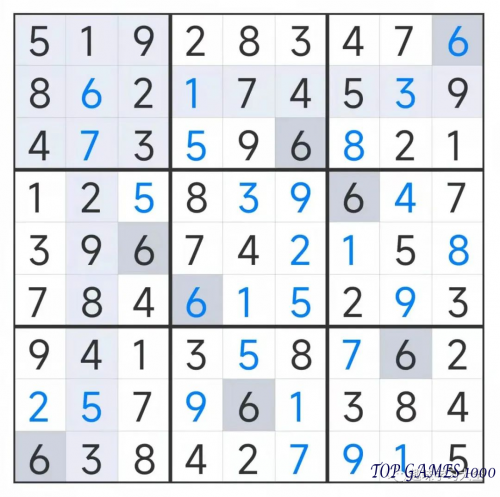
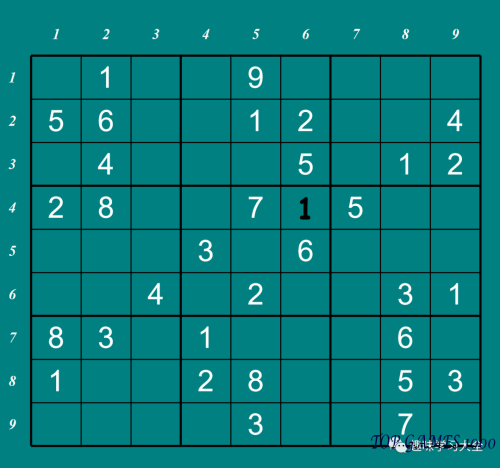
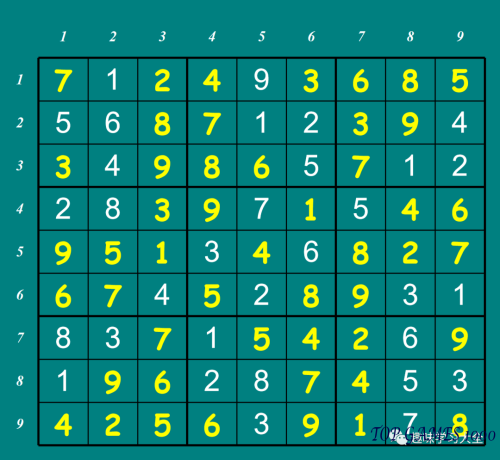
Sudoku Answers
Sudoku Solution Techniques:
- Sole Candidate Method: If a cell’s row, column, and sub-grid already have 8 different numbers and there is only one number left to fill, that remaining number can be placed in the cell.
This method is relatively basic, and is illustrated below with the following examples.
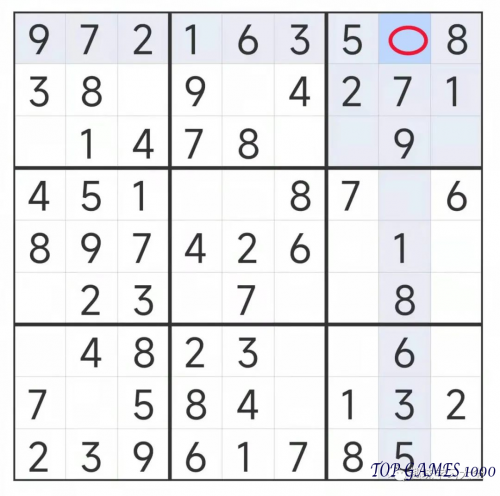
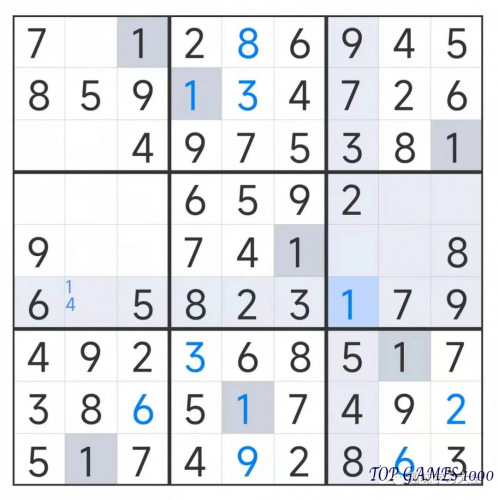
There is no number 4 in the same row as the red square in the grid, please fill in 4.
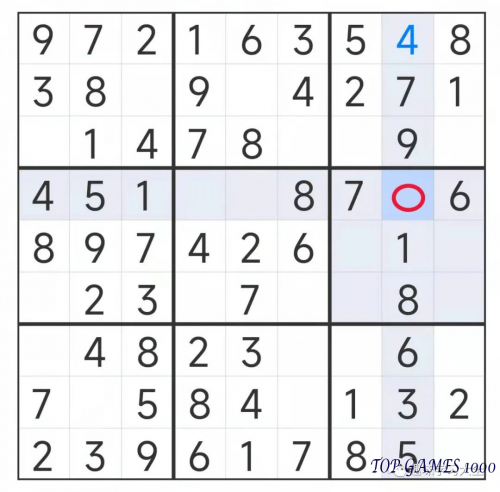
In the same column as the red-circled square, the number 2 has not yet appeared. Therefore, fill in the red-circled square with the number 2.
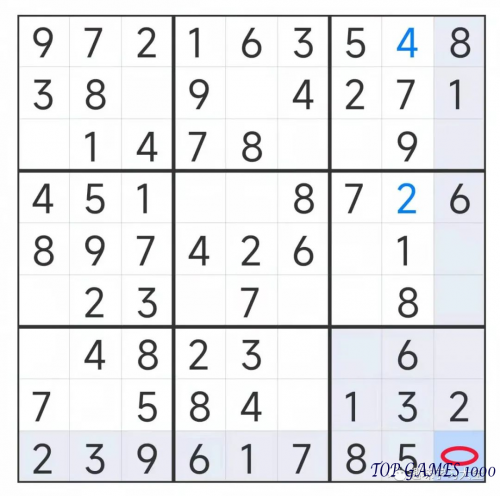
In the same row with the red square, there is no number 4, please fill in 4.

Sudoku Solution Techniques:
- Two-String Kite Method: When only two cells are left unfilled in a row, column, or sub-grid, the numbers in those two cells can be deduced by excluding them from the numbers in the corresponding row, column, or sub-grid.
The answer to this puzzle is not provided, as it is up to you to solve using techniques such as the two-string kite method.
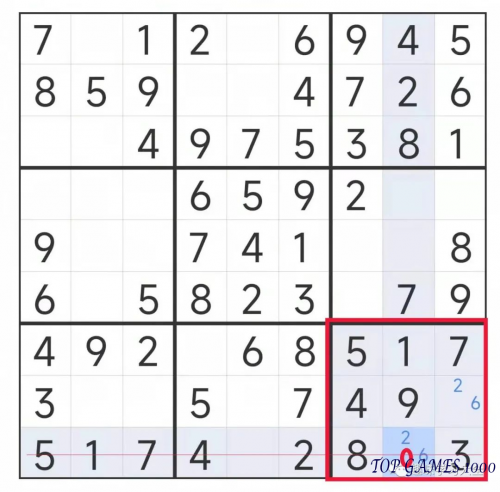
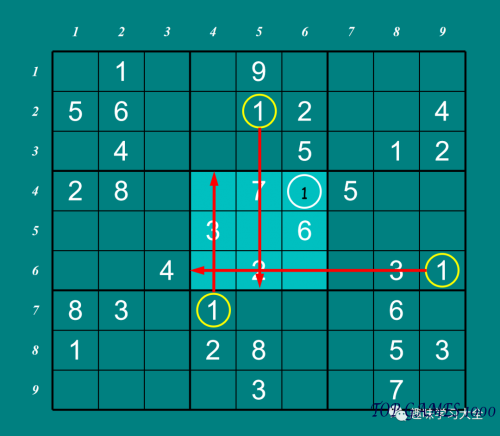
In this sub-grid, two squares can only be filled with the numbers 2 or 6. There is already a 2 in the corresponding row, so the number 2 can be excluded from the possibilities in this sub-grid. Therefore, the red-circled square can only be filled with the remaining number, 6.
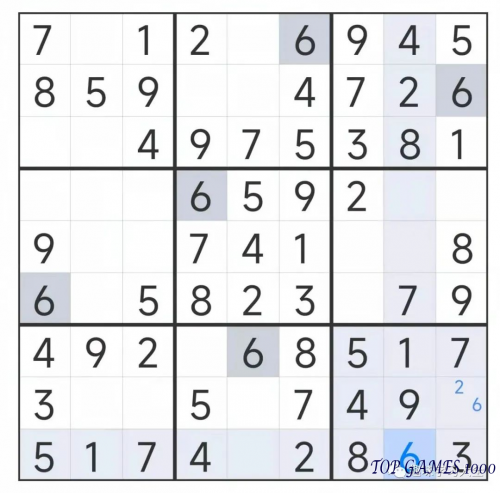
Fill in the number 6.
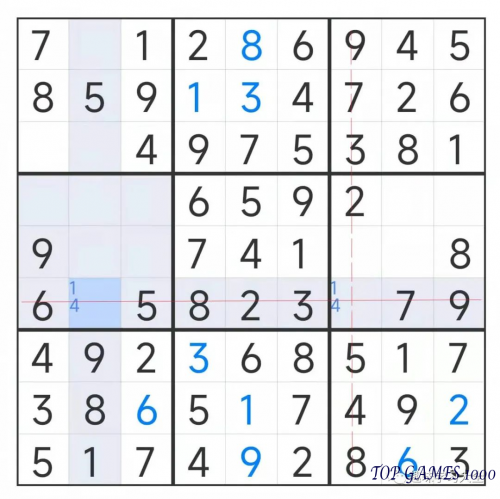
Two blank squares in the row with the horizontal line can only be filled with the numbers 1 or 4. Since there is already a 4 in the corresponding column, the number 4 can be excluded from the possibilities in the intersection of the two lines. Therefore, the only remaining option is to fill that square with the number 1.
Fill in the number 1.
Sudoku Solution Techniques:
- Sub-Grid Exclusion Method: This method involves using numbers to find out which squares in a sub-grid can be filled with numbers. The sub-grid exclusion method is the most commonly used and intuitive solution technique in the solving process.
Puzzle/Problem
After excluding the row and column where the number 1 is already present, it can be deduced that the white-circled square in the sub-grid is the only location where the number 1 can be placed.
Continue to observe the row and column of the number 1 in the next sub-grid.
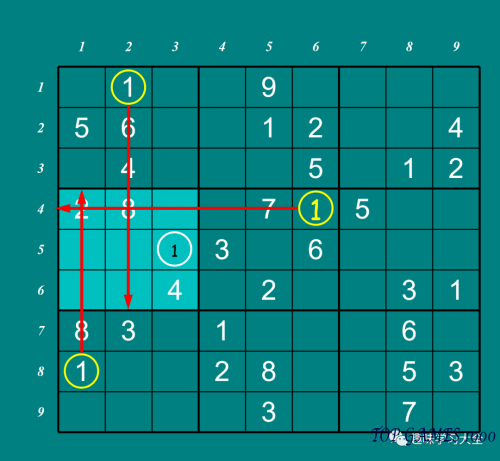
The number 1 can only be placed in the white-circled square of the sub-grid, based on the exclusion of its row and column.

Let’s continue to the next sub-grid.
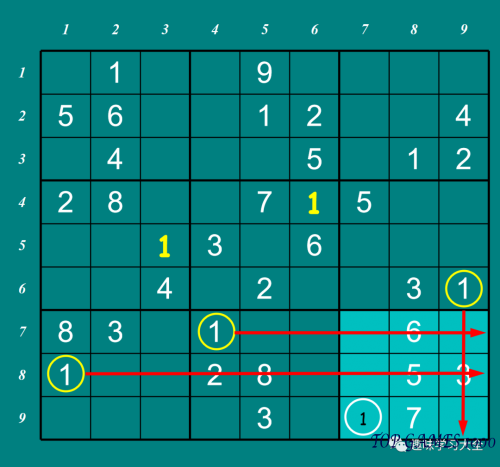
The number 1 can only appear in the white-circled square of this sub-grid.
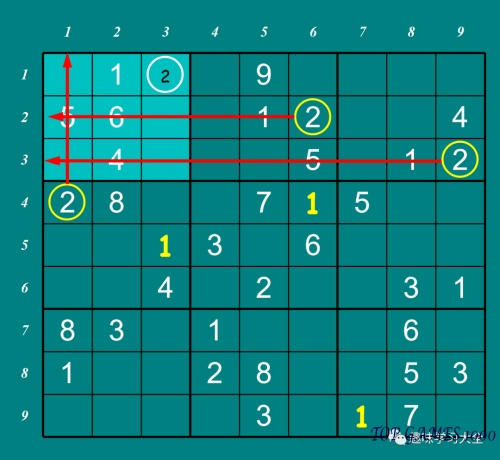
Sub-Grid Exclusion Method for Number 2 in the first sub-grid.
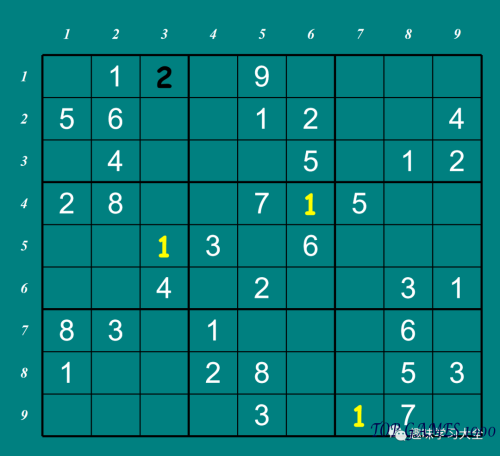
This method can be used throughout to solve the Sudoku puzzle.
Today we introduced these three basic Sudoku solution techniques. We will bring you more Sudoku solution techniques in the future. Stay tuned to our public account:
In order to better practice Sudoku puzzles, we recommend downloading the “Juzi Sudoku” app, which contains over 10,000 Sudoku puzzles of varying difficulty levels, suitable for long-term practice!
Apologies, the answer to the Sudoku puzzle was not provided in the text.