Sudoku Solving Technique: Row and Column Hidden Single

Row-column Hidden Single is an important tool for solving Sudoku puzzles. It refers to the combination of row exclusion method and column exclusion method. It uses the “no repetition” rule in Sudoku to determine the position of a number in a row or column by exclusion. Let’s learn this method through some simple examples:

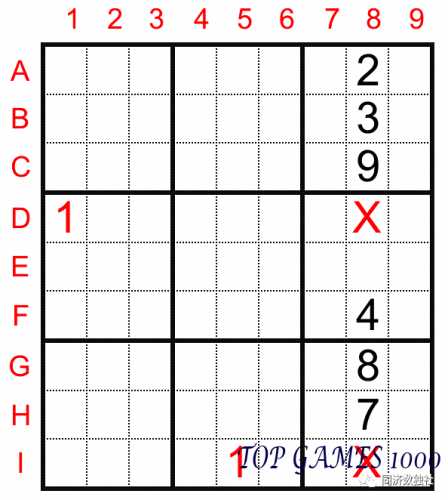
Looking at the position of number 1 in the 8th column, since numbers 1 already exist in cells D1 and I5, we know that digit 1 will not appear again in rows D and I. Therefore, we can exclude the possibility of 1 in cells D8 and I8. Therefore, the digit 1 in column 8 can only be in cell E8.

 

In this process, we used the column exclusion method for column 8, eliminating the “prohibited areas” of digit 1 one by one, and finally determining the position of 1 in column 8.

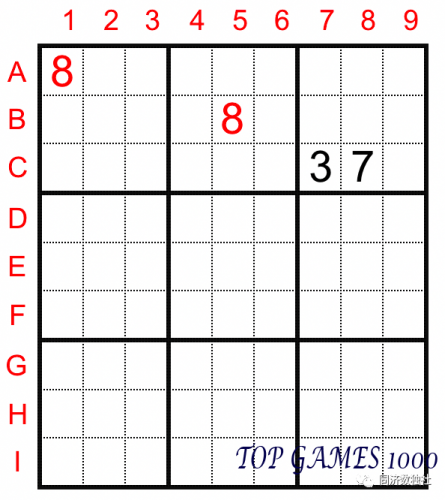
For the second example, we have two different observing methods:

We can use the box exclusion method introduced in the previous article. Look at the third box, since A1=B5=8, the number 8 in the third box can only be in cell C9.

Or, we can use the row exclusion method. Look at row C, since A1=8, cells C1, C2, and C3 cannot be 8. Similarly, based on B5=8, we can exclude cells C4, C5, and C6. Since cells C7 and C8 have already been occupied by other numbers, we know that the digit 8 in row C can only be in cell C9.

Through this example, we can also see that if there is a step in the puzzle solving process where both the box exclusion method and row-column exclusion method can be used, the box exclusion method is often more intuitive and clear. This is why the box exclusion method has become the most basic and widely used technique in Sudoku. In contrast, the observation difficulty of the row-column exclusion method is generally higher than that of the box exclusion method.

Let’s take a closer look at the row-column exclusion method through a practical example:

This is an entry-level puzzle with multiple methods that can be used. Here are some examples of using row-column Hidden Single:

Observe the position of number 1 in column 1. Since D7=G9=1, we can exclude the possibility of 1 in cells D1 and G1, so F1 must be 1.

Observe the position of number 4 in row G. Since I2=4, we can exclude the possibility of 4 in cells G1, G2, and G3. Additionally, since D6=4, we can also rule out G6. So the digit 4 in row G must be in cell G8.

Observe the position of number 2 in column 3. Based on B2=H1=2, we can constrain the digit 2 in the fourth box. Then we know that D3=2 based on E9=2.

In the previous article, we mentioned that if the box exclusion method is used, it is best to observe the box with the most digits first. Similarly, if row-column exclusion method is used, it is best to start with rows or columns that have the most digits (generally, rows or columns with at least 5 known numbers can be considered “more digits”).

In this example, columns 4 and 6 already have 6 known digits, so we should prioritize observing these two columns:

Column 4: Since F6=1, we can exclude the possibility of 1 in cells E4 and F4, so the digit 1 must be in cell B4. Then we can continue to use the row-column exclusion method for column 4 based on E7=3, and we can deduce that F4=3 and E4=6.

Column 6: We need to find the position of number 4. Since I4=D7=4, we know that E6=4. Also, based on G4=8, we can determine that the digit 8 in column 6 is located in cell D6. Then we know that H6=2.

In addition to the row-column exclusion method, readers can also try using the Naked Single introduced in previous articles to fill in all the digits in columns 4 and 6.

Therefore, for rows or columns with many known digits, we can combine the only possibility rule and the row-column exclusion method. These two methods provide different observation perspectives and can complement each other, thereby improving the efficiency of puzzle solving.

This completes the introduction of the basic techniques for standard Sudoku puzzles. Many beginners may feel confused even though they understand the techniques. This is a normal phenomenon, and many Sudoku masters have experienced this stage. To overcome this dilemma, the most direct and effective method is to practice more puzzles that are appropriate for their level, improve their sensitivity to these solving techniques, and achieve a qualitative improvement through a quantitative accumulation of experience.