Sudoku Solving Technique: Naked Single

The rule of standard Sudoku is to fill in each empty cell with a number from 1-9, so that each row, each column, and each 3×3 box contains unique numbers.

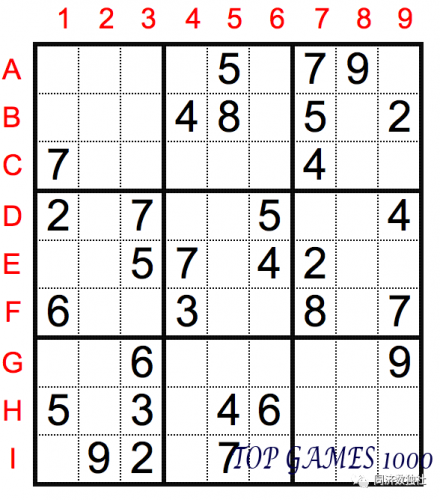
In the following figure, the second box already has 8 numbers, and since the numbers in each box can’t repeat, the number in cell B6 can be uniquely determined as 4.

A simple analysis just now actually embodies the basic idea of the sole candidate technique: when a row, a column or a box already has 8 numbers, the remaining number can be uniquely determined. This technique is called the sole number method and is a special case of the sole candidate technique.

The Naked Single is essentially an extension of the sole number method. Its method is as follows: for a selected cell, if there are already 8 different numbers in the same row, same column and same box as it, then this cell can only be filled with the remaining number.

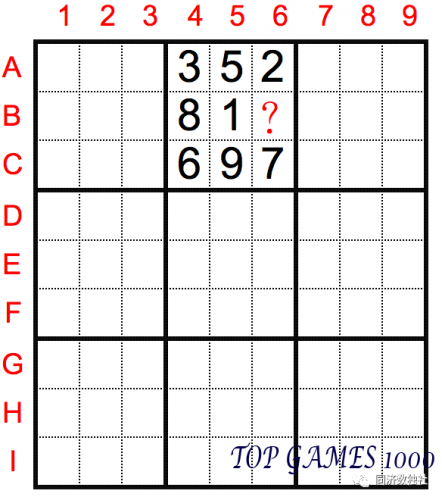
Let’s take an example:

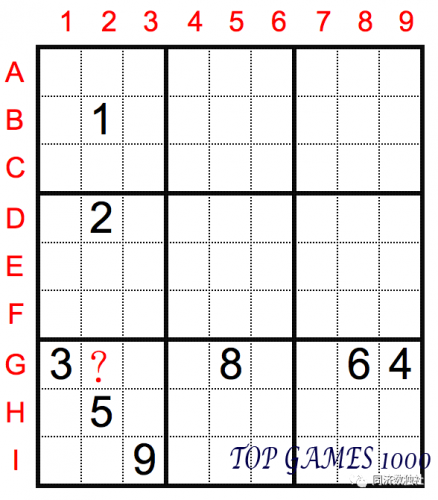
Observe cell G2. In the same box (the 7th), there are numbers 3, 5 and 9; in the same row, there are numbers 4, 6, and 8; in the same column, there are numbers 1, 2, and 5. According to the standard Sudoku rule, we know that the number in cell G2 can’t be the same as any of these numbers, so G2 must be 7.

Above is a simple introduction to the sole candidate technique. Now let’s take a look at an example in practice, where you can try to find which cells can be solved using this technique:

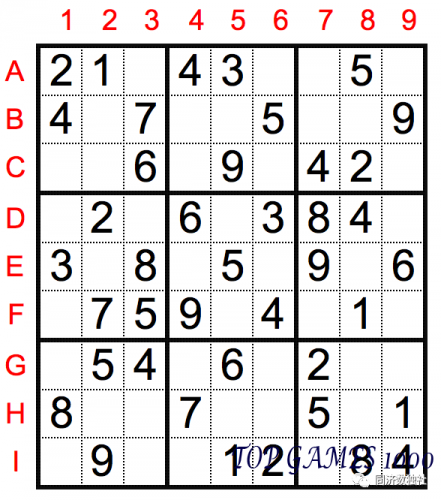
This is a beginner-level (lower than entry-level) standard Sudoku puzzle with a lot of given numbers, so many cells can be solved using the sole candidate technique. Here are a few examples:

C1=5 (there are 2469 in the same row, 38 in the same column, and 17 in the same box as C1)

D5=7 (there are 23468 in the same row, 19 in the same column, and 5 in the same box as D5)

F7=3 (there are 4579 in the same row, 28 in the same column, and 16 in the same box as F7)

I3=3 (there are 12489 in the same row and 567 in the same column as I3)

H6=9 (there are 1578 in the same row, 234 in the same column, and 6 in the same box as H6)

……

In this example, there are many cells that can be solved using the sole candidate technique. But for some puzzles, it can be quite difficult to find a breakthrough using only this technique. Let’s look at the example below and try to find the cells that can be solved using the sole candidate technique: (the answer will be revealed later)

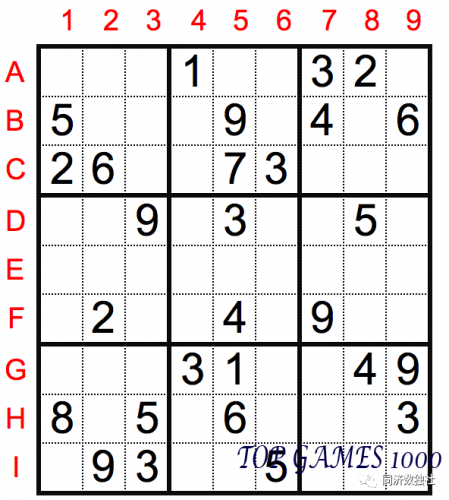
The answer is here: (there is only one cell that can be directly solved using the sole candidate technique in this puzzle)

Observe cell G2. There are numbers 1, 3, 4, and 9 in the same row; numbers 2, 6, and 8 in the same column; and numbers 3, 5, 8, and 9 in the same box. By the sole candidate technique, G2 must be 7.

From the above example, we can see that although the principle of the Naked Single is easy to understand, it can be difficult to apply in real-life puzzles due to the complexity of numbers on the grid. Therefore, the key to improving Sudoku skills is to practice more and develop a sensitivity to techniques through careful observation.

Finally, let’s look at another example where there is only one cell that can be solved using the sole candidate technique: