Sudoku solving technique introduction: Block Hidden Single

The rule of standard Sudoku is to fill in numbers 1-9 in the blank cells, so that each row, each column, and each box contains no duplicate numbers. A box refers to the nine 3×3 square areas enclosed by bold lines.

The Block Hidden Single is one of the most important, basic, and widely used techniques in standard Sudoku, which determines the position of a number in a box by exclusion. Let’s learn about the box exclusion technique through some simple examples:

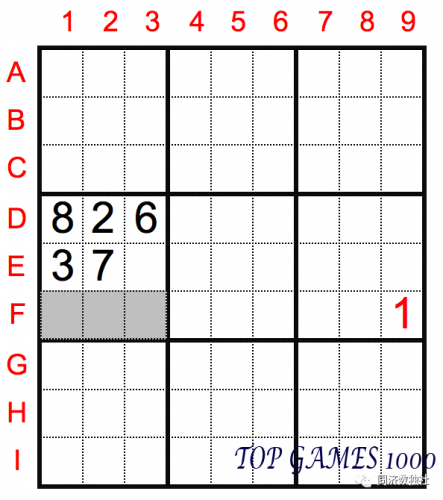
In the example above, we can observe the position of number 1 in the fourth box. Since F9=1, the three gray cells in the same row, F1, F2, and F3, become the “prohibited area” for number 1, so the number 1 in the fourth box can only be filled in cell E3.

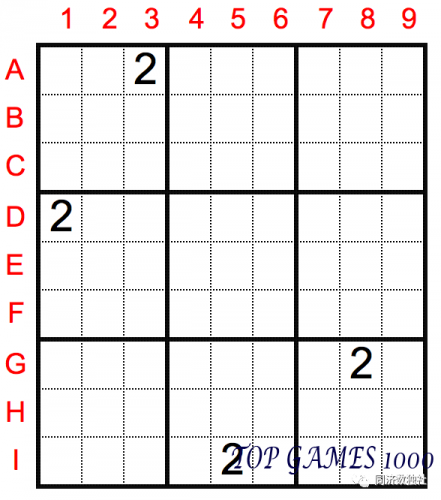
In the example above, only four 2’s are given, without any other numbers, but we can still use the box exclusion technique to determine a number: Look at the seventh box, and due to the existence of these four 2’s, the number 2 in the seventh box can only be filled in cell H2.

Generally speaking, the higher the frequency a number appears, the greater the possibility of continuing to use the box exclusion technique to determine that number. (Of course, this is not absolute, but a general trend.)

Let’s now look at a practical example:

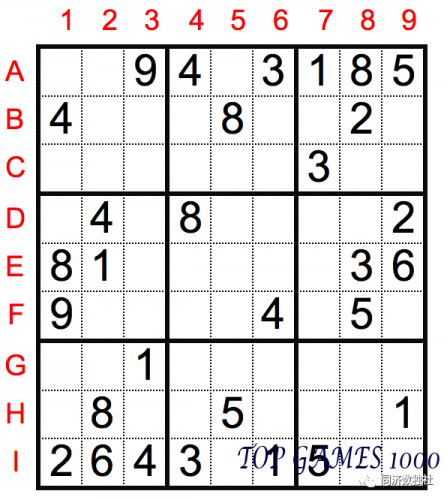
Since numbers 1, 4, and 8 appear frequently, we can start with these three numbers and try to solve them using the box exclusion technique. Here are a few examples (methods are not unique):

Number 1: Look at the sixth box. Given A7 and H9 are 1, we can obtain D8=1.

Number 4: Look at the eighth box. Given A4 and F6 are 4, we can obtain G5=4.

Number 8: Look at the first box. Given B5, E1, and H2 are 8, we can obtain C3=8.

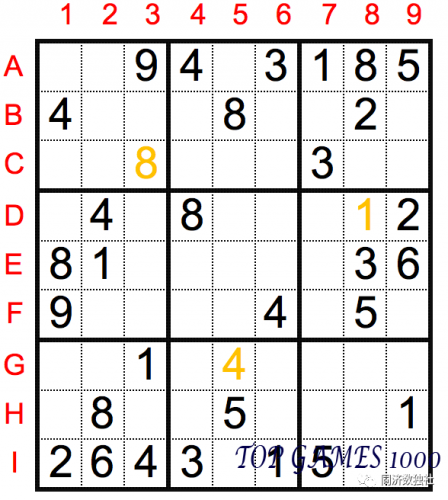
After identifying the numbers in a block using the block exclusion method, it is worthwhile to observe if the same number appears consecutively.

For example, in the previous example, we identified that D8=1. At this point, there were already six 1s on the board, with only three remaining. In this scenario, we can continue using the block exclusion method for 1, until all 1s have been placed on the board.

Let’s take a look at a practical example:

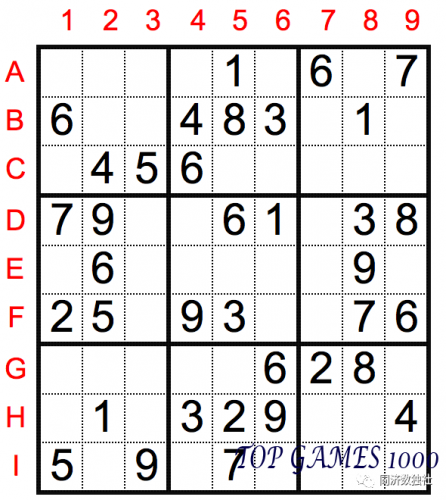
The difficulty of the puzzle is not too high, and there are still many opportunities to use the block exclusion method. Here are a few examples:

[1] Observing the sixth block, we can deduce that E9=2 based on the information G7=2.

[2] Observing the second block, we can deduce that C6=7 based on the information A9 and I5=7.

[3] Observing the second block, we can deduce that C5=9 based on the information F4 and H6=9.

For the second block and sixth block that we chose, there were already five known numbers, making it a block with many known numbers. For the remaining numbers in the block, there were fewer spaces to choose from, which makes the use of the block exclusion method more effective.

Therefore, when using the block exclusion method, in addition to observing frequently appearing numbers, we can also observe blocks with many known numbers, in order to increase the efficiency of identifying numbers.

When solving Sudoku puzzles, different people have different observation methods, which can lead to different sequences and methods of identifying numbers. For instance, in the following example:

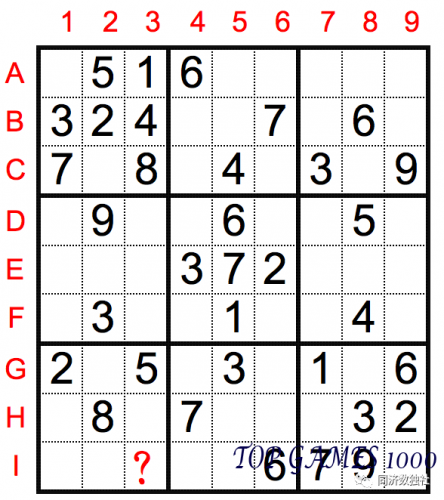
For the cell marked with a question mark, if we observe it using the block exclusion method, based on the information of B1, F2, and H8, we can deduce that I3=3. However, we can also use the unique residue method introduced in the previous article, to observe other numbers in the same row, column, and block as I3. According to the unique residue method, we can deduce that I3=3, since the number 3 is the only remaining number that can be placed in the block, row, and column that hasn’t already been used.

When it comes to different techniques for solving Sudoku puzzles, there is no one “best” method. The effectiveness of different methods can vary depending on the individual player’s familiarity with them, and their usage habits during the solving process. However, there is no single technique that can solve all Sudoku puzzles, as many of the more challenging problems require the use of a combination of methods. Therefore, to improve your Sudoku solving skills, you not only need to be familiar with common techniques (such as the block exclusion method), but also not overlook the importance of combining multiple techniques.

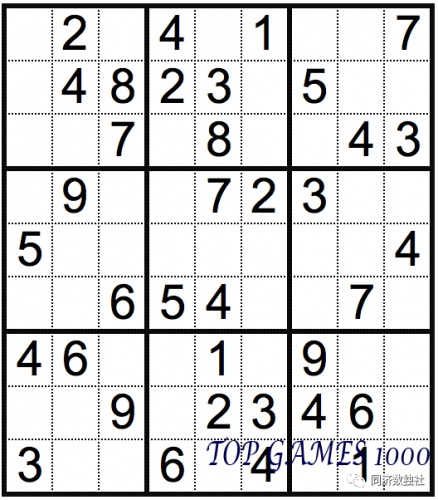
Finally, here is a practice question that can be solved solely using the block exclusion method (though of course, you can use any method you prefer):